朝闻道

这篇文章主要是介绍Fisher Information，也称费雪信息。

basics

fisher information，记为$I_X(\theta)$, 产生的随机变量X的参数$\theta$的费雪信息。其数学表示式写为期望：

$I_X(\theta) = E_X((\frac{d}{d\theta}\log f(x|\theta))^2) = \int_X (\frac{d}{d\theta}\log f(x|\theta))^2p_\theta(x)dx)$

上式中微分表达 $\frac{d}{d\theta} \log f(x | \theta)$被称之为score function, 用来描述参数变化时模型的敏感度（f函数值变化程度）。
从这个数学表达上看fisher information在局部最优时可以看作score function的二阶矩. 此外因为在局部最优点，其期望为0则可以推断fisher information时score function的方差。

$I_X(\theta) = E_X(S(x, \theta)^2) - 0 = E_X(S(x, \theta)^2) - E_X(S(x,\theta))^2 = \text{VAR}(S(x, \theta))$

因此费雪信息可以用来估计MLE估计结果处score function， 也就是log likelihood梯度的方差

如果对n个iid的X抽样做建模，$I_{X^n}(\theta) = n I_X(\theta)$, 因此$I_X(\theta)$被称之为单位费雪信息. 这个等式表明，对于同一个分布，采样次数越多，对参数估计准确率越高，信息也就越多。

此外，费雪信息在密度函数满足一定的平滑条件时，可以写为：

$I_X(\theta) = - E_X(\frac{d^2}{d\theta^2}\log f(x|\theta)) = - \int_X \frac{d^2}{d\theta^2}\log f(x|\theta) p_\theta(x)dx$

二阶导在几何角度看描述了函数的弯曲程度，也就是函数在该点凸（二阶导大于等于0）和凹（二阶导小于等于0）的程度。这里也就是描述了log likelihood在局部最优的情况，越大说明在局部最优的弯曲程度大，置信区间越窄，数据越可信。

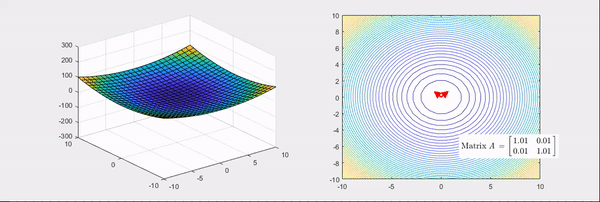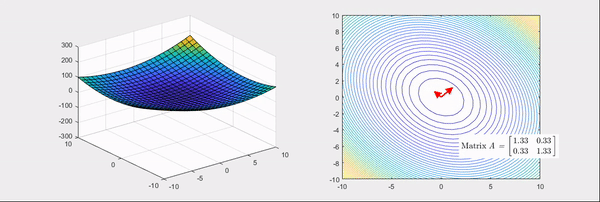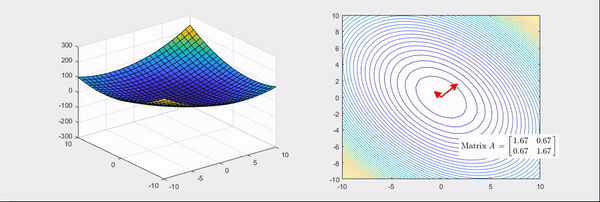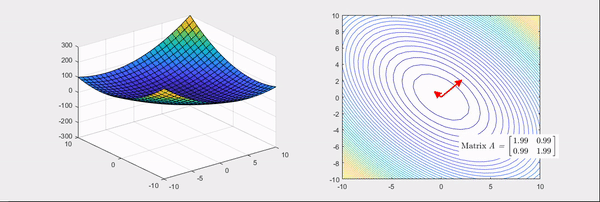
从这个角度再看上面的定义，所谓log likelihood梯度的方差，只有再弯曲程度越大的地方周围区域梯度会剧烈变化，方差很大。这个角度看，两个定义本质一致，平滑条件是为了满足任意阶可导。

在针对高维数据计算费雪信息时，其结构呈矩阵称之为Fisher Information Matrix. 这种情况下，矩阵可以写为:

$I_X(\theta) = E_X(\nabla \log f(X|\theta) \nabla \log f(X|\theta)^T) = - E_X(H_{\log f(X|\theta)})$

与参数估计的联系：Cramér–Rao lower bound

对于通过MSE做无偏估计获得的参数，受Cramér–Rao lower bound定理约束，满足以下大小关系：

$\text{VAR}(T) \geq \nabla \phi (\theta)^T I_\theta^{-1}\nabla \phi (\theta)$

表达式中$\phi(\theta)$表示生成数据的统计量函数，而$T$表示对该函数的无偏估计。
这样当我们带入函数$\phi(\theta) = \lambda \theta$时，$\nabla \phi (\theta)=\lambda$, 相应表达式变成$\text{VAR}(\lambda T) \geq \lambda^T I_\theta^{-1}\lambda$, 这样最终获得针对无偏估计得到参数的不等式：

$\text{Cov}(T) \geq I_\theta^{-1}$

此外，参考Detian Deng大神的回答，MLE估计到的参数渐进分布的方差是$I_\theta^{-1}$。记为：

$\sqrt{n}(\theta_{\text{MLE}} - \theta) \rightarrow N(0, I_\theta^{-1})$

与KL散度的联系：二阶近似

在一定的平滑条件下，可以建立KL散度与Fisher Information之间的关系：

$KL(P_{\theta_1} \big| \big| P_{\theta_2}) \simeq \frac{1}{2} (\theta_1 - \theta_2)^T I_X(\theta_1) (\theta_1 - \theta_2)$

定义自然梯度

借助这一性质，在信息几何中定义出自然梯度，相对于欧氏空间中的梯度计算：

$\lim\limits_{\epsilon \rightarrow 0} \argmin\limits_{\big| d \big| \leq \epsilon} L(\theta + d)$

上式可以解释为：向参数空间上某d向量方向走出欧氏空间测量的一小步，使Loss function 更小，选取其中效果最好的d更新参数

信息几何在概率空间使用KL散度作为距离调整了参数更新的目标：

$\lim\limits_{\epsilon \rightarrow 0} \argmin\limits_{KL(\theta \big| \big| \theta + d) \leq \epsilon} L(\theta + d)$

也就是向参数空间上某d向量方向走出概率空间测量的一小步，使Loss function 更小，选取其中效果最好的d更新参数

写为拉格朗日乘子为：

$\min L(\theta + d) + \lambda (KL(\theta \big| \big| \theta + d) - \epsilon) \simeq L(\theta) + \nabla L(\theta)^Td + \lambda (\frac{1}{2} d^TI_X(\theta)d - \epsilon)$

对右边针对变量d做梯度，并使梯度为0，则获得$\nabla L(\theta) + \lambda I_X(\theta)d = 0$
从而推得$d = -\frac{1}{\lambda} I_X^{-1}(\theta) \nabla L(\theta)$
这样我们获得自然梯度的常用定义：

$\widetilde{\nabla} h = I_X^{-1} \nabla h$

References

• A Tutorial on Fisher Information - Alexander Ly
• New Insights and Perspectives on the Natural Gradient Method - James Martens
• Stanford Statistics 311 - Chapter 8 Fisher Information
• 费雪信息 (Fisher information) 的直观意义是什么？- Detian Deng
• 如何知道Cramér–Rao lower bound是可以取得的（它就是最小的）？- 覃含章回答
• Geometric Meaning of Hessian Matrix
• Natural Gradient Works Efficiently in Learning

Photo by National Cancer Institute on Unsplash