朝闻道

实践中的梯度下降算法(Gradient Descent), 一般指Batch Gradient Descent, SGD两种.
在深度学习中，SGD是最简单常用的优化器，随着深度学习发展，针对SGD在learning rate的选择和控制方面的优化，以及深度学习理论的理解增强。其优化器变种层出不穷，有里程碑意义的包括 Momentum, AdaGrad, RMSprop, Adam. 以及Transformer训练中常用的AdamW. 这些最流行的优化器一般都是一阶优化器。实际上目前还有一些二阶优化器比如很多深度学习框架也可以支持，比如K-FAC。去年谷歌也放出来一篇在深度学习中使用二阶优化器的实验论文 Scalable Second Order Optimization for Deep Learning。

这篇博文结构如下，我们先回顾下深度学习优化算法的主要挑战，然后分别介绍下一阶和二阶优化器的研究进展。

---

优化器设计的挑战

深度学习中的优化任务有以下几个特点：

• 优化代理损失函数：在深度学习训练时，我们会设计相应的损失函数作为优化目标，对于其中不可导也、难以优化的目标常转为其代理损失函数，比如0-1 loss转为NLL loss.
• 间接优化：希望在训练集数据上优化，最终在测试集获得最优效果
• 非凸优化：与SVM这种基于凸优化理论基础的算法不同，深度学习的损失函数很多时候是非凸的(参考神经网络的损失函数为什么是非凸的?)

在深度学习中处理非凸优化时，会把非凸问题当作很多个凸优化处理求解，也就是求多个局部最优获得全局最优的思路。因此，这些优化算法的理论证明部分，一般只在凸函数证明其收敛性。

在deeplearningbook中介绍了以下一些优化器的设计挑战：

• ill-conditioning 深度学习中的病态问题
  • 对于微小的输入扰动，损失函数就会发生巨大的变化，这种情形称之为病态。反之则为良态
  • 如果学习中出现病态问题，为了避免损失函数大幅度扰动并逐渐收敛，每次迭代必须要使用尽量小的learning rate去平衡，导致学习停滞。
• 局部最小
  • 非凸优化不能保证损失函数的局部最小就是全局最小。
• 台面、鞍点等平面
  • 鞍点在高维中比局部最小更常见，且梯度为0，有时在一些平面点上甚至Hessian matrix也都是0。
  • 被困在参数空间的这种地方比落入局部最小更可怕，损失函数值更大。
• 悬崖与梯度爆炸
  • 一般用gradient clipping可以解决梯度爆炸问题
• 长距离依赖
  • RNN中比较常见的问题
• 不准确的梯度
  • 大部分batch-based方案都只能估算梯度，无法获得参数空间上的准确梯度。此外训练数据本身也可能包含一些噪音
• 局部结构与整体结构相关性差：
  • 很多优化算法只能根据局部信息做优化，所以导致无法找到参数空间上的全局最优。

这些挑战也时评价优化器和策略时常常考察的方面。

---

一阶优化器

GD、MBGD，SGD

梯度下降是直接从凸优化中借鉴来的优化算法。整体思路是每次对全部的训练数据计算平均梯度，然后更新参数：

$\theta = \theta - \eta \nabla_\theta J(\theta, X, Y)$

而MBGD和SGD分别是梯度下降的小批量版本和随机采样版本。小批量版本主要是为了降低梯度计算时的内存消耗做的优化，而随机采样则是再小批量版本基础上增加了每次批数据采样时的随机性。

Momentum

Momentum,也被称为SGDM，在SGD基础上添加了动量。这里的动量指每次参数更新部分，都由上一轮的更新部和本轮的梯度构成中：

$v_t = \gamma v_{t-1} + \eta \nabla_\theta J(\theta, X, Y)$

$\theta = \theta - v_t$

这里的$\gamma$是momentum term，一般设定为0.9

AdaGrad, RMSprop

AdaGrad是一个可以自动根据参数进行学习适应的优化算法，对于更新已经很多的参数使用较小的学习率，对于很少更新的参数使用更大的学习率。

$\theta = \theta - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla_\theta J(\theta, X, Y)$

其中矩阵 $G_t \in \Reals^{d \times d}$ 是一个diagonal matrix，对角线上是对应维度参数过去所有梯度（包含本轮梯度）平方和。$\epsilon$是防止分母为0添加的数字，一般是1e-8.

RMSprop是对AdaGrad的一个改进，主要针对学习率在AdaGrad中因为梯度累计学习率单调下降问题，使用滑动平均代替了全部梯度平方和。

$G_t = \lambda G_{t-1} + (1 - \lambda) g_t^2$

这里的$\lambda$一般设定为0.9

Adam, AdamW

Adam融合了前面提到的Momentum和自适应学习率。首先计算动量和梯度平方的滑动平均：

$m_t = \beta_1 m_{t-1} + (1 - \beta_1) g_t$

$v_t = \beta_2 v_{t-1} + (1 - \beta_2) g_t^2$

考虑到$m_t, v_t$初始化都是0，且当$\beta_1, \beta_2$接近1时，动量和梯度平方的滑动平均一开始都会很小。这里为了规避这样的bias问题，对上面的值做了一个比例调整：

$\widehat{m}_t = \frac{m_t}{1-\beta_1^t}$

$\widehat{v}_t = \frac{v_t}{1-\beta_2^t}$

可以看到，随着t的增大，比例调整趋近于1. 最后在参数更新上参考AdaGrad

$\Theta = \Theta - \frac{\eta}{\sqrt{\widehat{v}_t} + \epsilon}\widehat{m}_t$

而AdamW相比Adam增加了weight decay。一般情况下，我们会认为weight decay与L2 regularization效果相同，都是在梯度计算上做修改，即$g_t = \nabla_\theta J(\theta, X, Y) + \lambda \Theta$，但这个表达式实际上是L2 regularization的效果。而weight decay策略可以整理为$\Theta = (1-\lambda)\Theta - ...$。L2正则在Adam中恰恰不能整理为这种weight decay形式，两者并不等价。
在AdamW中，就是这样做的，其参数更新写为

$\Theta = (1-\lambda)\Theta - \frac{\eta}{\sqrt{\widehat{v}_t} + \epsilon}\widehat{m}_t$

Demon

Demon，又称Decaying momentum algorithm，一种动量策略，可以搭配各种包含动量的优化算法使用，比如Adam和SGDM。
这个策略主要是针对这些算法中的momentum term做调整，在上文中的SGDM中写为$\gamma$。数学表达如下：

$\beta_t = \beta_{init} \frac{1 - \frac{t}{T}}{(1-\beta_{init}) + \beta_{init}(1 - \frac{t}{T})}$

表达式中的$(1-\frac{t}{T})$表示剩余迭代比例。这个函数值被限制在0与1之间，逐渐缩小至0.

---

二阶优化器

二阶优化器优点是可以用更少的迭代次数进行优化，但很多机器学习中的常用二阶优化器被高维场景下的计算量所限制，无法应用于深度学习。

Hinton的学生James Martens基于自然梯度提出了可用于深度学习训练的K-Fac，以及后续的分布式训练方案等等，他目前在Deepmind任职，他在去年的Deepmind的深度学习视频课程Deepmind x UCL中专讲优化算法部分。
尽管在收敛速度上有优势，但K-Fac实际上并没有火起来，具体原因可以参考知乎问题：为什么K-FAC这种二阶优化方法没有得到广泛的应用？.
后面谷歌做了Shampoo，并在最近发了改进版的论文。这里我们学习下K-Fac与Shampoo的理论部分，作为正式介绍论文内容的引子。

牛顿法

牛顿法是我们入门最常见的二阶优化器，它来自泰勒二阶展开的微分表示：

$f(x) = f(x' + \triangle x) \simeq f(x') + f'(x')\triangle x + f''(x')\triangle x^2 /2$

因为局部最优梯度为0，所以对上式做微分可以得：

$f'(x) = f'(x') + f''(x') \triangle x = 0$

$x_n = x_{n-1} - \frac{f'(x_{n-1})}{f''(x_{n-1})}$

在高维问题中写为：$x_n = x_{n-1} - \lambda H^{-1}(x_{n-1})J(x_{n-1})$, 其中$\lambda$表示步长。

牛顿法确实在二次性强的函数上优化速度上拔群，但是存在以下几个问题：

• 需要保证Hessian存在且可逆，且随着参数增加Hessian Matrix的维度爆炸
• 牛顿法需要初始点离局部极小值不要太远：对于任何一个极小值，都存在一个领域满足Hessian可逆且Lipschitz连续
• 牛顿法只有在Hessian是正定矩阵时，才能保证迭代沿数值下降方向优化。

拟牛顿法

针对牛顿法的问题，诞生了高斯-牛顿法和LM算法。
高斯-牛顿法使用泰勒一阶展开进行最小二乘法的优化。对于最小二乘优化

$x = \argmin \frac{1}{2} ||f(x)||^2 =\argmin\frac{1}{2} (f(x') + J(x')\triangle x)^2$

针对$\triangle x$求导使其导数为0，可得

$J(x)^TJ(x)\triangle x = - J(x)^T f(x)$

这样令$H=J^TJ, B=-J^Tf$，可以获得$H\triangle x = B$
这样参数的更新公式为$x_n = x_{n-1} - ((J^TJ)^{-1}J^Tf )(x_{n-1})$
在迭代过程中，参数更新直到$\triangle x$足够小.
而广义最小二乘法/最小平方在优化问题中，f(x)一般写为$f(x)=y-g(x)$, 最小化的目标是优化标签与特征函数的差值。
而最小二乘法从统计角度可以视为一种MLE参数估计方法，其优化过程可以看作：对于假设数据与模型预测结果的残差，这一统计量，假设其分布是正态分布时进行MLE参数估计。这是一个基于中心极限定理的合理假设，最小二乘法也在因此在非线性优化中居于核心地位。
高斯牛顿将Hessian Matrix的求解转化为Jacobian Matrix的矩阵运算，可以起到不错的提速效果。

LM算法全称Levenberg–Marquardt algorithm，针对上面的最小二乘法的优化问题做了补充。主要是改善牛顿法和高斯牛顿的不稳定性问题：当初始值离局部最小较远时，无法保证收敛。
LM算法在Hessian矩阵中加入了阻尼系数控制每次迭代的步长和方向：

$(H + \lambda I)\triangle x = B$

$x_n = x_{n-1} - ((J^TJ + \lambda I)^{-1}J^Tf )(x_{n-1})$

当$\lambda$参数大时，迭代方向趋近于梯度下降的方向；越小则趋近于高斯牛顿的方向。
求解过程中，每次进行参数调整会先尝试计算下一迭代参数, (一般情况 $\alpha = 0.1, \beta = 10$)

• 如果新参数没有使残差大小$\sum_i r_i^2$下降则增大超参数$\lambda = \beta \lambda$重新求解下一迭代参数，并重新做判断。
• 如果残差大小下降, 则接受参数更新，并减小超参数$\lambda = \alpha \lambda$

LM算法是二阶优化器中最流行的一种，应用于谷歌的优化库Ceres Solver中。

K-Fac

K-Fac建立在信息几何方向的自然梯度（就是陈默大佬说的："信息几何得出的最有用的概念"）理论基石上。自然梯度的概念建立在Fisher Information之上，数学表达为:

$\widetilde{\nabla} h = I_X^{-1}(\theta) \nabla h$

其中$h$是目标函数而$I_X(\theta)$是fisher information， 费雪信息这个概念可以参考另一篇博文Short Introduction to Fisher Information， 作为本文参考。

基于费雪信息和自然梯度构建的自然梯度下降法$\widetilde{\nabla} h = I_X^{-1} \nabla h$中， 主要挑战是计算Fisher Information的逆矩阵。这里作者搭建了一个简单的神经网络阐述K-Fac的原理，其结构如下：

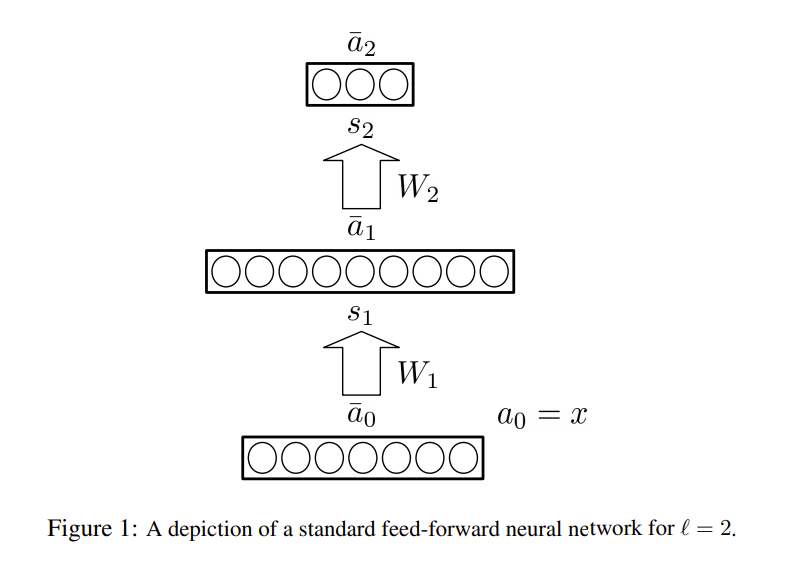
K-Fac在Loss为Negative Log-likelihood的假设下，直接使用其Gradient计算Fisher Information，形为:

每一个$W_i$表示i层的参数向量，Fisher Information被写为各层参数梯度两两相乘的积。
各层参数在做反向传播时，某一层的参数梯度，一般通过上一层单位输出和反向传递函数输出的导数相乘得到： $DW_i = \frac{\partial L}{\partial W_i} = \frac{\partial L}{\partial S_i}\frac{\partial S_i}{\partial W_{i}} = g_i a_{i-1}^T$
后续作者通过把向量外积推广为更广义的Kronecker积，对Fisher Information的计算进行了近似化简，构造为Khatri-Rao积的形式：

中间近似相等这一步比较粗糙，但是实践效果还不错，所以被保留下来。
这样，神经网络的Fisher Information Matrix可以由以上方法分层求解、按块构建出来。
但在进行自然梯度下降时，近似估计Fisher Information Matrix的逆矩阵才是关键。在逆矩阵求解上作者考虑了两种近似方式：

• 把$I_X(\theta)$简化为一个块对角线矩阵，然后使用Kronecker积的性质$(A \otimes B)^{-1} = A^{-1} \otimes B^{-1}$ 直接计算Fisher Information的逆矩阵。这样转化为分层的逆矩阵运算。逆矩阵运算可以通过SVD来求解。
• 把$I_X(\theta)$简化为一个三对角线矩阵。这部分计算复杂一些，但是相比上一种方案，近似效果更好一些。

最终算法方案参考了LM算法中阻力系数的更新方式，并对参数更新量加入了Momentum机制。更新参数step简述如下：

• 反向传播过程计算：$\nabla h, A, G$,
• if step % T1 == 0: update $I_X^{-1}(\theta)$ with $A,G$
• 自然梯度计算: $\widetilde{\nabla} h = ( I_X^{-1}(\theta) + \lambda)\nabla h$
• if step % T2 == 0: update $\lambda$ with LM style rule
• 使用momentum策略进行参数更新

Shampoo

Shampoo算法与AdaGrad紧密相关，这里的AdaGrad不是我们常用的版本，而是其论文中提到但是没有广泛应用的 full-matrix version of AdaGrad。这样一个思想来源让它不同于上面说的K-Fac，作为AdaGrad优化之作，Shampoo更方便在深度学习中使用。

在AdaGrad论文中，我们常用的版本是为了方便深度学习场景而做的近似方案：取$G_t=G_{t-1}+\text{diag}(g_tg_t^T)$。这个方案借助对角矩阵的性质对后续$G_t$矩阵的幂运算和逆运算进行优化，一方面保留了部分二阶信息 gradient variance (参考高斯牛顿) ，另一方面在计算上和存储上非常友好(空间时间复杂度都是$O(d)$)。

相比full-matrix version of AdaGrad 保存一个巨大的$d \times d$大小的covariance矩阵，并针对其做幂运算和逆运算。Shampoo在每个参数的每个维度上单独计算preconditioner，大幅降低了存储和计算压力。

对于多维参数的gradient（k个维度），Shampoo给每一个维度都单独计算并缓存了一个可累计的Preconditioner $H_i$, dim=$(n_i, n_i)$。
对待gradient的每个维度逐个计算：

1. 先将参数进行维度变化为$G_i$, dim=$(n_i, -1)$
2. preconditioner computaion： 更新该维度的$H_i = H_i + G_iG_i^T$
3. preconditined gradient computation： $G_i = H_i^{-\frac{1}{2k}}G_i$
4. 最后将参数维度恢复正常，准备下一个维度上的计算。

所有维度遍历后，使用最终的gradient进行参数更新。

Shampoo算法中涉及到对矩阵的负幂，论文中使用SVD分解在对角矩阵上进行计算。大量存储preconditioner，外加逐个在每个参数的每个维度上运算SVD，最终限制了Shampoo算法在更大规模的深度学习模型上的使用。

Updated Shampoo

Scalable Second Order Optimization for Deep Learning这篇论文主要是基于实验结果对Shampoo做了优化，使之能适用于更大规模的深度学习任务。

优化包含以下几个方面：

• preconditioner复杂度
  • 针对Embedding层，可以直接跳过超大维度的preconditioner和preconditioned gradient计算
  • 针对包含超大tensor的FFN， 可以把大张量拆分成多个小张量运算
  • preconditioner计算频率可以适量降低（比如1000steps一次），直到明显影响优化结果
• SVD复杂度：使用the coupled Newton iteration algorithm替换，这个运算过程需要双精度。
• 混合计算：考虑到preconditioner需要双精度运算，在每N steps计算时，由多个CPU并行计算，再将参数转到GPU，用于后续参数更新。

这些优化加持下，Shampoo可以用于Bert-Large这种目前主流大模型的训练。收敛加快而每step的运算速度方面相比一阶算法也没有明显的劣势。下图，学者在使用Transformer model训练机器翻译模型过程中，Shampoo相比Adam、AdaGrad加速效果显著。

---

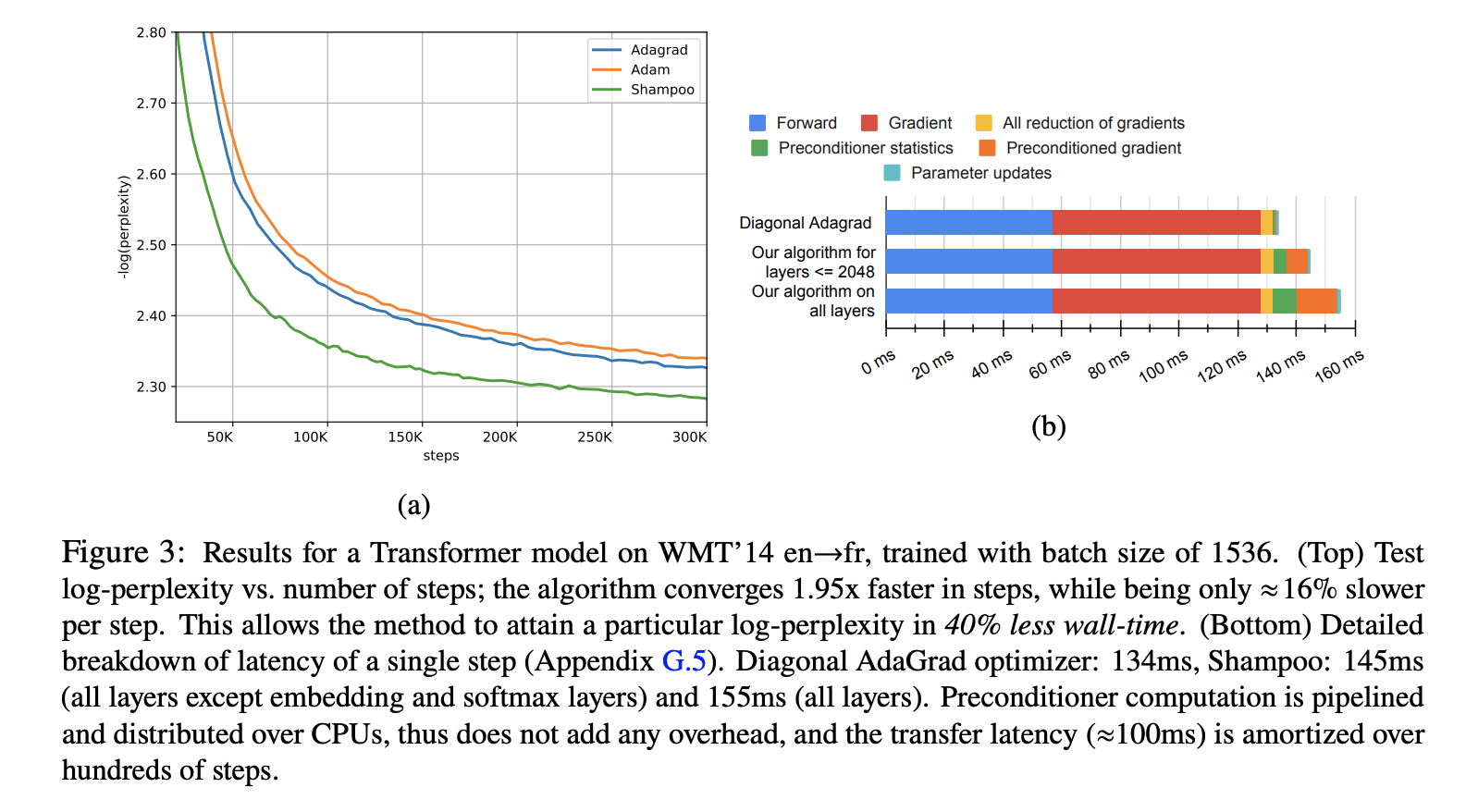
References:

• An overview of gradient descent optimization algorithms - Sebastian Ruder
• An updated overview of recent gradient descent algorithms - John Chen
• A Survey of Optimization Methods from a Machine Learning Perspective - Shiliang Sun
• deeplearningbook
• Scalable Second Order Optimization for Deep Learning - Rohan Anil
• 病态问题及条件数
• 高斯-牛顿法(Guass-Newton Algorithm)与莱文贝格-马夸特方法(Levenberg–Marquardt algorithm)求解非线性最小二乘问题
• 非线性优化之高斯牛顿法、L-M 算法
• New Insights and Perspectives on the Natural Gradient Method - James Martens
• Optimizing Neural Networks with Kronecker-factored Approximate Curvature - James Martens
• A Tutorial on Fisher Information - Alexander Ly
• 2nd-order Optimization for Neural Network Training
• Shampoo: Preconditioned Stochastic Tensor Optimization - Vineet Gupta
• Adaptive Subgradient Methods for Online Learning and Stochastic Optimization - John Duchi
• COS 597G: Toward Theoretical Understanding of Deep Learning - Lecture 5: Adaptive Regularization (Fall 2018)

Photo by Daniel Frank on Unsplash